量子力学では、位置に関するシュレディンガー方程式を用いて、量子に関する多くの問題を解くことができる。その例として、今回は井戸型ポテンシャルを扱う。
井戸型ポテンシャルの例
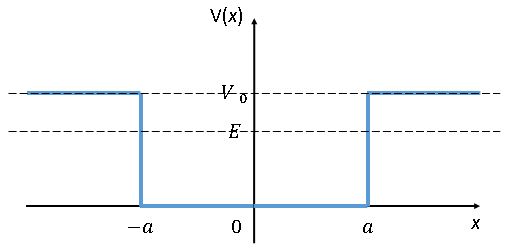
図1の様な井戸型ポテンシャルを考える。
これは非常にオーソドックスな井戸型ポテンシャルで、注目する点は固定されたポテンシャルの大きさV0に対して、エネルギー固有値EがV0よりも大きいか、小さいかの2パターンで場合分けをする必要がある。
エネルギーEがV0よりも低い場合は、波束が-a~aの範囲に拘束されるが、V0よりも大きい場合はどの位置でも波束が観測できると言う状態である。
まず、位置xを変数とする波動関数を∅(x)とすると、時間に依存しないシュレディンガー方程式は、
$$H\emptyset\left(x\right)=E\emptyset\left(x\right)$$
$$\left(-\frac{ħ^2}{2m}\frac{∂^2}{∂x^2}+V(x)\right)∅(x)=E∅(x)\qquad(1)$$
とする。ここで、区間x<-aにおけるポテンシャルをV(x)=V0とし、-a<x<aのときV(x)=0、またx<aのときV(x)=V0とする。よって、各区間におけるポテンシャルを(1)に代入すると、それぞれの区間における波動関数が求められる。また、波動関数は位置が∞の場合は値が0となる有解条件があるので、xが±∞の項は0になる必要がある。ゆえに、以上を考慮すると、
ⅰ) x<-aのとき
$$\emptyset_1\left(x\right)=Ae^{\rho\ x}\qquad(2)$$
(このとき、(2)に x=-∞ を代入すると0となるので、有界条件を満たす。)
ⅱ) -a<x<aのとき
$$\emptyset_2\left(x\right)=Be^{ikx}+Ce^{-ikx}\qquad(3)$$
また、ekxについてオイラーの公式を用いると、
$$\emptyset_2\left(x\right)=B^\prime\sin{kx}+C^\prime\cos{kx}\qquad(4)$$
ⅲ) a<xのとき
$$\emptyset_3\left(x\right)=De^{-\rho\ x}\qquad(5)$$
このとき、kとρの値は、
$$k=\sqrt{\frac{2mE}{ħ^2}}\qquad(6)$$
$$\rho=\sqrt{\frac{2m(V_0-E)}{ħ^2}}\qquad(7)$$
とした。次に、波動関数の連続性を保つため、接続条件を考える。まず、x=-aにおいてΦ1(-a)=Φ2(-a)と、傾きが等しくなる条件Φ1‘(-a)=Φ2‘(-a)を満たせばよい。ゆえに、
$$Ae^{-\rho\ a}=Be^{-ika}+Ce^{ika}\qquad(8)$$
$$A\rho\ e^{-\rho\ a}=Bike^{-ika}-Cike^{ika}\qquad(9)$$
となる。また、x=aにおける接続条件はΦ2(a)=Φ3(a)、Φ2‘(a)=Φ3‘(a)なので、
$$De^{-\rho\ a}=Be^{ika}+Ce^{-ika}\qquad(10)$$
$$-D\rho\ e^{-\rho\ a}=Bike^{ika}-Cike^{-ika}\qquad(11)$$
となる。次に、(8)と(9)により、Aを消去して整理すると
$$B\left(ik-\rho\right)e^{-ika}=C\left(ik+\rho\right)e^{ika}$$
$$C=\frac{ik-\rho}{ik+\rho}Be^{-2ika}\qquad(12)$$
となる。また、(10)と(11)によりDを消去すると
$$B\left(ik+\rho\right)e^{ika}=C\left(ik-\rho\right)e^{-ika}\qquad(13)$$
となる。ここで、(13)に(22)を代入してCを消去して整理すると
$$\left(k^2-\rho^2\right)\left(e^{2ika}-e^{-2ika}\right)=2ik\rho\left(e^{2ika}+e^{-2ika}\right)$$
$$\left(k^2-\rho^2\right)\sin{\left(2ka\right)}=2k\rho\cos{\left(2k\rho\right)}$$
$$\tan{\left(2ka\right)}=\frac{2k\rho}{k^2-\rho^2}\qquad(14)$$
となり、タンジェントの形で図示する事ができる。
また、ポテンシャルが軸を中心に対称の場合には簡単に解くことができる。具体的にはポテンシャルが対称となる場合は、奇関数または偶関数となる性質を利用することで、計算量を減らす事ができる。具体的な手順として、シュレディンガー方程式の解が奇関数または偶関数であることの確認から始める。
まず、ポテンシャルが左右対称と仮定することより、V(x)=V(-x)とする。ここで、シュレディンガー方程式は
$$-\frac{ħ^2}{2m}\frac{∂^2∅(x)}{∂x^2}+V(x)∅(x)=E∅(x)\qquad(15)$$
であり、x → -x とし、ポテンシャルの対称性を用いると
$$-\frac{ħ^2}{2m}\frac{∂^2∅(-x)}{∂x^2}+V(x)∅(-)x=E∅(-x)\qquad(16)$$
となる。これにより、Φ(x)とΦ(-x)は、共に固有値Eの固有関数だと言える。また、一つの固有エネルギーに対し、一つの固有関数が対応するので、Φ(x)とΦ(-x)の間に定数倍の関係があると考えられる。ゆえに、その比例定数をcとすると、
$$\emptyset\left(-x\right)=c\emptyset\left(x\right)\qquad(17)$$
となる。ここで、x → -xとすると、
$$\emptyset\left(x\right)=c\emptyset\left(-x\right)\qquad(18)$$
となり、(18)に(17)を代入すると、
$$\emptyset\left(x\right)=c^2\emptyset\left(x\right)$$
$$∴c=\pm{1}\qquad(19)$$
となる。よって、
$$\emptyset(-x)=\pm\emptyset\left(x\right)\qquad(20)$$
となりΦ(x)=Φ(-x)の場合は偶関数、Φ(x)=-Φ(x)の場合は奇関数となる。ここで、
に(20)の結果を用いると、偶関数の条件を満たす場合、(4)は、
$$\emptyset_2\left(x\right)=C\cos{kx}\qquad(21)$$
となり、cosで表現できる。また、その微分は、
$${\emptyset_2}^\prime\left(x\right)=-kC\sin{kx}\qquad(22)$$
となる。これを用いてx=aにおける接続条件を考えるとΦ3(a)=Φ2(a)より、
$$De^{-\rho\ a}=C\cos{ka}\qquad(23)$$
となり、
$$-\rho De^{-\rho a}=-kC\sin{ka}\qquad(24)$$
となる。ゆえに、(24)に(23)を代入して整理すると
$$\tan{ka}=\frac{\rho}{k}\qquad(21)$$
となる。(14)と(25)を比較すると(25)の方がグラフを簡単に書く事ができるので、これを用いてグラフを書く事を考える。まず、ka=α、ρa=βとすると(25)は
$$\alpha\tan{\alpha}=\beta\qquad(26)$$
と書き換える事ができる。ここで、縦軸をβ、横軸をαの系を考える。この系上の円はエネルギーを用いて表現でき、
$$\alpha^2+\beta^2=\frac{2mV_0a^2}{ħ^2}\qquad(27)$$
となる。よって、(26)と(27)の関数の接点が解となる。また、奇関数の場合も同様に接続条件を用いて解くとsin関数で表現できる。結果として、エネルギー固有値は、基底状態のとき半波長となり左右対称の偶関数、第一励起状態のときは1波長のため奇関数、第二励起状態で3/2波長となり偶関数と、半波長ずれるごとに偶関数と奇関数を交互に変化していく。
無限井戸型ポテンシャル
有名なポテンシャル問題の例として、無限の深さの井戸型ポテンシャルを考える問題がある。
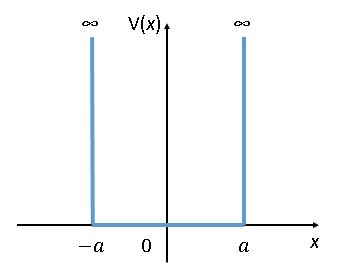
ここで、x=±aにのみV(±a)=∞のポテンシャルが存在する場合を考える。このとき、大きさが無限の2つのポテンシャルに電子が囲まれて閉じ込められているので、-a<x<a の範囲以外では波動関数は0になると解釈できる。ここで、波動関数は
$$\frac{\partial^2\emptyset\left(x\right)}{\partial\ x^2}=-\frac{2mE}{ħ^2}∅(x)\qquad(28)$$
となり、
$$k=\sqrt{\frac{2mE}{ħ^2}}\qquad(29)$$
とすると
$$\frac{\partial^2\emptyset\left(x\right)}{\partial\ x^2}=-k^2\emptyset\left(x\right)\qquad(30)$$
となる。よって、波動関数は
ⅰ) x<-aのとき
$$∅_1(x)=0\qquad(31)$$
ⅱ) -a<x<aのとき
$$∅_2(x)=Be^{ikx}+Ce^{-ikx}\qquad(32)$$
ⅲ) x<aのとき
$$∅_3(x)=0\qquad(33)$$
となる。次に、波動関数の接続条件を考える。まず、x=aにおいて、∅2(a)=∅3(a)を考えると
$$Be^{ika}+Ce^{-ika}=0\qquad(34)$$
となる。また、x=-aにおいて、∅2(-a)=∅1(-a)を考えると
$$Be^{-ika}+Ce^{ika}=0\qquad(35)$$
となる。よって、(34)と(35)によりCを消去して整理すると
$$B\left(e^{2ika}-e^{-2ika}\right)=0\qquad(36)$$
となり、sin の公式を用いると
$$2iB\sin{2ka}=0$$
$$∴ \ \sin{2ka}=0\qquad(37)$$
となる。ゆえに、この式が成立するために、2kaが満たす条件は、
$$2ka=0,\pi\ ,\ 2\pi,\cdots\cdots\qquad(38)$$
である。これにより、波数は基底状態をn=0として
$$k_n=\frac{\left(n+1\right)\pi}{2a}\ \left(n=0,\ 1,\ 2,\cdots\cdots\ \right)\qquad(39)$$
となる。ここで、(29)に(39)を代入して整理すると、エネルギーは、
$$E_n=\frac{ħ^2}{2m}{k_n}^2=\frac{π^2ħ^2(n+1)^2}{8ma^2} (n=0,1,2,⋯⋯)\qquad(40)$$
となる。
次に、第n励起状態の固有関数をΦn(x)として、基底状態(n=0)の固有関数Φ0(x)と、第1励起状態(n=1)の固有関数Φ1(x)を求める。まず、基底状態の固有関数Φ0(x)を求める。(39)にn=0 を代入すると波数は
$$k_0=\frac{\pi}{2a}\qquad(41)$$
となる。よって、 (34)を(32)に代入してCを消去し、
$$\begin{align}\emptyset_n\left(x\right)&=Be^{ik_nx}+Ce^{-ik_nx}\\&=Be^{ik_nx}+\left(-Be^{2ik_na}\right)e^{-ik_nx}\\&=B\left(e^{ik_nx}-e^{2ika}e^{-ik_nx}\right)\qquad(42)\end{align}$$
に(41)を代入し、オイラーの等式を用いると、
$$\begin{align}\emptyset_0\left(x\right)&=B\left(e^{i\frac{\pi}{2a}x}-e^{2i\frac{\pi}{2a}a}e^{-i\frac{\pi}{2a}x}\right)\\&=B\left(e^{i\frac{\pi}{2a}x}-e^{i\pi}e^{-i\frac{\pi}{2a}x}\right)\\&=B\left(e^{i\frac{\pi}{2a}x}+e^{-i\frac{\pi}{2a}x}\right)\\&=2B\ cos\left(\frac{\pi}{2a}x\right)\qquad(43)\end{align}$$
となる。ここで、式に対して-a~a の範囲で規格化すると、
$$\int_{-a}^{a}{\left|\emptyset_0\left(x\right)\right|^2dx}=1$$
$$\left(2B\right)^2\ \int_{-a}^{a}\left|\cos^2\left(\frac{\pi}{2a}x\right)\right|dx=1$$
$$\left(2B\right)^2\ \int_{-a}^{a}\frac{cos\left(\frac{\pi}{a}x\right)+1}{2}dx=1$$
$$\left(2B\right)^2\ \left[\frac{\frac{a}{\pi}sin\left(\frac{\pi}{a}x\right)+x}{2}\right]_{-a}^a=1$$
$$\left(2B\right)^2\ a=1$$
$$2B=\frac{1}{\sqrt a\ }\qquad(44)$$
となる。これを(43)に代入すると
$$\emptyset_0\left(x\right)=\frac{1}{\sqrt a\ }cos\left(\frac{\pi}{2a}x\right)\qquad(45)$$
となり、規格化された基底状態の波動関数が求められた。また、同様の手法で第1励起状態の波動関数を求めると、
$$\emptyset_1\left(x\right)=\frac{1}{\sqrt a\ }sin\left(\frac{\pi}{2a}x\right)\qquad(46)$$
となる。最終的には、全てのnについて波動関数を求めると
$$\emptyset_n\left(x\right)=\begin{cases}\frac{1}{\sqrt a}cos(\frac{(n+1)π}{2a}x) & (nが偶数のとき)\\\frac{1}{\sqrt a}sin(\frac{(n+1)π}{2a}x) & (nが奇数のとき)\end{cases} \qquad(47)$$
となる。
第6章 変数分離法 第8章 波動関数の反射と透過 物理学入門
#井戸型ポテンシャル #シュレディンガー方程式 #波動関数 #境界条件 #偶関数 #奇関数 #量子力学


コメント